Для тех, кто не любит математику. Или как вывернуть сферу наизнанку.

Великий математик Давид Гильберт сказал однажды, что математическую теорию можно считать совершенной лишь тогда, когда ее удается изложить первому встречному. Последователи Гильберта приходят в полное отчаяние, пытаясь жить по этому рецепту. Математика все более специализируется, и сейчас ученому математику порой стоит большого труда даже своим коллегам объяснить суть решаемых им задач. Однако время от времени исследования в ведущих и, казалось бы, недоступных пониманию отраслях этой науки приводят к открытию, которое интересно для непрофессионала и в то же время может быть объяснено без чрезмерного упрощения. Поразительный пример этого — теорема Стефена Смейла о так называемых регулярных отображениях сферы, опубликованная в 1959 г.

Область, в которой тогда работал Смейл, — дифференциальная топология — одна из самых абстрактных отраслей современной математики. Тем удивительнее, что все-таки удалось придумать наглядное объяснение одному из самых поразительных следствий из теоремы Смейла. А именно, можно продемонстрировать, как надо выворачивать сферу наизнанку.

В обычном смысле это, конечно, невозможно: сферу обязательно пришлось бы разорвать. Но в дифференциальной топологии разрешается — мысленно, разумеется,— протаскивать поверхность сквозь самоё себя — таковы «правила игры» в этой науке. Но тогда сразу бросается в глаза простое решение.

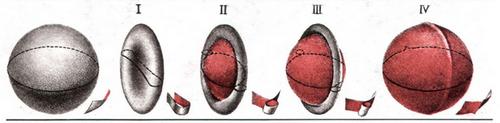
Надо сжимать противоположные стороны к центру, пока они не пройдут друг сквозь друга (I). Внутренняя, окрашенная поверхность (II) проступает с двух противоположных краев. Продолжим этот процесс «вытягивания» внутренней поверхности до тех пор, пока колечко, образованное оставшейся частью внешней поверхности (II), совсем не исчезнет. К несчастью, при этом процессе колечко образует тугую петлю (III), которую приходится затянуть. В результате получается рубец (IV), а это не удовлетворяет дифференциальных топологов, потому что они рассматривают только так называемые «гладкие поверхности», у которых нет никаких углов и изломов.

Итак, задача состоит в том, чтобы вывернуть наизнанку сферу таким образом, чтобы, избавляясь от колечка, не получить рубца. И здесь интуиция снова подсказывает, что задача неразрешима. Когда Смейл впервые объявил, что он может доказать существование решения, то ему никто не поверил. Но интуиция была неправа: в доказательстве Смейла не нашлось ни одной логической ошибки. Математики убедились, что теоретически возможно проследить доказательство шаг за шагом и найти явное описание деформации, выворачивающей сферу. Но это было столь сложно, что казалось безнадежным делом. В течение некоторого времени после открытия Смейла было известно, что в принципе можно вывернуть наизнанку сферу без рубца, но никто не имел ни малейшего представления, как это осуществить.

Но, в конце концов, математики с этой задачей справились. Как — поймете, рассмотрев рисунки. Они занимательны.

Хотя доказательство Смейла не состояло из одних рисунков. Любопытно, что в его работе их вообще нет — слишком уж сложны те фигуры, которые в неявном виде содержатся в его абстрактном аналитическом аппарате. Их не удалось бы изобразить самому изобретательному художнику — фантазия математиков поразительна. Но, пожалуй, еще более поразительна их способность передавать друг другу самые сложные идеи, не прибегая к рисункам. История с выворачиванием сферы — яркое тому свидетельство. Она стала известной широкой публике благодаря французскому топологу Рене Тома, который узнал о ней от своего коллеги Бернара Морена, а тот, в свою очередь, — от американца Арнольда Шапиро, изобретателя этой «выворотки». Вот это особенно любопытно, если учесть, что Бернар Морен слеп.

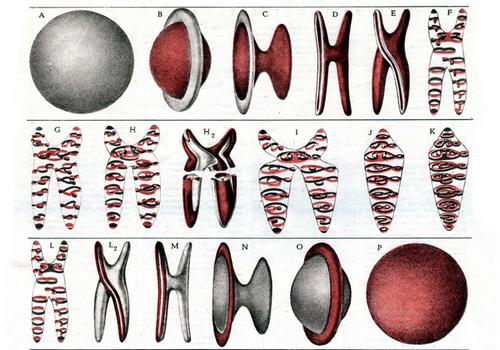
На этих картинках показано, как можно вывернуть сферу наизнанку, и при этом не нарушить требований дифференциальной топологии. Сначала надо сблизить противоположные стороны серой сферы (А), продавливая их друг сквозь друга. Тогда с двух сторон проступает окрашенная поверхность (В). Затем надо растянуть один из окрашенных кусков (С) таким образом, чтобы получить поверхность, напоминающую седло на двух «ногах» (О). Эти две ноги перекручивают против часовой стрелки и получают поверхность Е. Она же показана снова (Р) «в разрезе» с помощью ленточек, которые, как и в «сфере с рубцом», изображают поперечные сечения на десяти различных уровнях.

Дальше нет смысла изображать получающиеся на каждом этапе поверхности — уж слишком они сложны. Но можно, если угодно, рассмотреть ленточки на всех 10 уровнях и мысленно дорисовать. Один этап (H2) мы все-таки решили показать — просто, чтобы можно было себе представить, каков тип получающихся фигур. Поверхность G появляется после сжатия и вращения на 90° седла поверхности Р.

Еще несколько шагов. А именно: между этапами I и J две одинаковые по форме ноги проходят друг сквозь друга. У каждого лентообразного сечения поверхности на этапе J есть две серые стороны, обращенные друг к другу. Между этапами J и К внутренний слой расширяется, а внешний сжимается; получается поверхность К — совершенно такая же, как J, но только цвета поменялись местами.

Дальше все действия идут в «обратном порядке». Вы можете составить о них представление, рассматривая картинки I, Н, С и т. д. Нужно только менять местами цвета ленточек на каждой картинке. Окончание этого второго ряда картинок мы приводим. Поверхность L соответствует поверхности F, L2 — Е, и т. п.

Окрашенная сфера (поверхность Р) соответствует серой сфере (поверхности А). Итак, деформация выполнена, и рубца нет. Сама возможность этого трюка была впервые доказана С. Смейлом. А все последовательные этапы деформации придумал А. Шапиро…

Автор: Д. Рыжков.