Геометрия Вселенной

Прежде чем рассказывать о чем-то из области современной науки, надо условиться внимательно обдумывать все аргументы и по возможности не прибегать к слову «очевидно». Это — очень опасное слово. В древности казалось, очевидно, что Земля не может быть шаром. «Иначе,— говорили ученые — скептики, — люди с другой стороны должны были бы ходить вниз головой, и они бы упали — это же очевидно!» В наше время в школе без особого труда объясняют даже маленьким ученикам и ученицам, что Земля шарообразна, а не падают люди с нее потому, что понятия «верх» и «низ» на Земле не имеют абсолютного смысла и являются не вполне точным выражением направлений к центру планеты и от него. И нам теперь очевидно, что Солнце не может каждый вечер погружаться в мировой океан, который будто бы окружает Землю-блин, что Земля не может стоять на трех китах и т. д.

Не только физика выясняла, что природа устроена совсем не так, как «видят очи». К этому выводу приводит нас вся деятельность человека. Чтобы узнать свойства окружающего нас мира, надо тщательно переработать информацию, которую получают органы чувств. И самый главный урок, который дала нам природа, состоит в том, что только правильно поставленный опыт может выяснить физическую сущность явлений и что никакие теоретические построения, какими бы они ни казались очевидными, но могут без опыта ответить на вопросы, касающиеся устройства физического мира.

Если все, что здесь сказано, не вызывает возражений, мы можем перейти к нашей основной теме.

В школе учат геометрию Эвклида. Определяют точку, прямую, плоскость аксиомами и не замечают, что правильность описания этими аксиомами результатов измерений в реальном мире ниоткуда не следует. Позже эти аксиомы переносятся в механику, и опять вопрос о проверке их на опыте не выясняется. Но всякая теория должна быть проверена на опыте, и в особенности — выводы геометрии Эвклида. Действительно, откуда мы знаем, что сумма углов треугольника равна 180? Если измерить с большой точностью углы треугольника, построенного на футбольном поле, то это окажется так. Но если бы мы построили треугольник, поместив одну вершину на Северном полюсе, а две других — на экваторе (на долготе Гринвича и на 90 восточной долготы), то в таком треугольнике каждый угол будет равен 90° и, следовательно, их сумме — 270°.

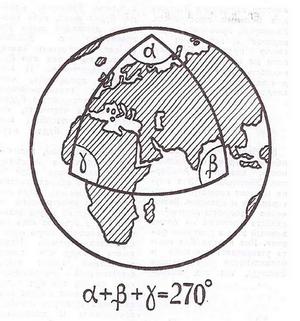
Могут возразить; в школьной теореме говорится о плоском треугольнике, а не о треугольнике, нарисованном на поверхности шара. Но, строя треугольник на поверхности Земли (для наглядности глобуса), мы тоже проводим «прямые линии» — кратчайшие между двумя точками линии на сферической поверхности. Это дуги большого круга.

Свойства поверхности шара, одно из которых мы сейчас рассмотрели, и образуют геометрию сферы. Мы видим, что геометрия сферы отличается от геометрии плоскости, и нетрудно понять, что каждая поверхность имеет свою геометрию. На примере суммы углов треугольника мы видим, кроме того, что можно изучать геометрию поверхности, не уходя с нее самой, а лишь измеряя характеристики фигур, нарисованных на ней. По крайней мере, в принципе можно получить все сведения о поверхности земного шара, производя на ней геодезическую съемку.

В МИРЕ ТРЕХ ИЗМЕРЕНИЙ

Мы сравнительно легко можем убедиться в разных свойствах сферы и плоскости. В трехмерном мире картина значительно сложнее. Зададимся снова вопросом: чему равна сумма углов треугольника, вершины которого лежат, например, на Солнце, Сириусе и на ближайшей к нам звезде — альфе Центавра. По геометрии Эвклида сумма углов треугольника равна 180. Но как проверить такое утверждение? Ссылка на то, что опыты на Земле подтверждают теорему, ничего не доказывает. Справедливое на малых расстояниях может оказаться неверным для больших.

На примере сферического треугольника мы видели, что отклонение от свойств плоских треугольников тем больше, чем больше треугольник. С другой стороны, у нас нет никаких способов измерить сумму углов такого большого треугольника. Более того, даже эти расстояния могут оказаться недостаточными, чтобы обнаружить отклонения от законов геометрии Эвклида. Отсюда следуют два вывода. Во-первых, у нас нет доказательств справедливости геометрии Эвклида для больших пространств. Во-вторых, проверить справедливость геометрии не так-то просто. Поэтому, если не ссылаться на очевидность, надо искать пути для экспериментального исследования вопроса.

ПРОСТРАНСТВО И ВРЕМЯ

Проблема была решена общей теорией относительности, созданной Альбертом Эйнштейном. Эта наука изучает геометрию пространства и времени. Включение в вопросы геометрии свойств времени — очень важный этап в развитии науки. Как нельзя без опыта утверждать что-либо о правильности геометрии Эвклида, так же, оказывается, у нас нет никаких оснований считать, что геометрические свойства нашего мира представляются одинаковыми движущемуся наблюдателю и наблюдателю, находящемуся в покое.

Специальная теория относительности установила, что движущиеся тела сокращаются в направлении движения. Поэтому измерение расстояния между двумя точками в пространстве с помощью натянутой веревки или же по времени, которое надо затратить для переезда из одной точки в другую с известной скоростью, дает разные результаты. Различие, правда, будет мало, если скорость движения мала по сравнению с 300 000 км/сек.— скоростью света, но, тем не менее, оно будет существовать. И мы должны предвидеть, что проверка геометрических свойств пространства будет зависеть, в частности, от того, каким способом мы эти свойства будем изучать.

Таким образом, геометрия и движение оказываются связанными друг с другом. Это обстоятельство и подразумевают, когда говорят, что пространство и время друг от друга зависят. Часто говорят еще о четырехмерном мире «пространство — время». Надо иметь в виду, что такое выражение имеет лишь формальный математический смысл, так как ясно, что ни в каких опытах или явлениях пространственные координаты и показания часов не могут быть перепутаны.

ПРЯМАЯ ЛИНИЯ

Чтобы изучать геометрию мира, надо, прежде всего, уметь провести прямую линию. Это можно сделать разными способами. Можно просто натянуть нитку между двумя точками. Можно прочертить прямую линию как траекторию тела, движущегося по инерции. Можно, наконец, прямой линией назвать путь луча света. В обычных, земных условиях мы должны следить, чтобы она не провисала, чтобы вес ее был мал и земное притяжение практически не изменяло ее форму. Наблюдая за движением тела, мы должны быть уверены, что на него не действуют никакие силы и оно действительно движется по инерции. Наконец, когда мы будем производить построение с помощью луча света, необходимо проверить оптическую однородность среды, чтобы быть уверенным, что свет не преломляется. Как бы мы ни начинали построение, мы сразу же уходим от чистой геометрии и должны производить настоящий физический опыт.

В таком опыте прежде всего обнаружится, что его результаты не абсолютно точны, а им сопутствует какая-то, пусть даже и очень небольшая, ошибка. В отличие от геометрических аксиом, которые точны по определению, геометрию реального мира мы определим лишь приближенно. Ясно, что, проводя опыт не в земных, а в космических условиях, трудно придерживаться всех перечисленных правил. Поэтому опыты должны быть поставлены так, чтобы они даже при небольшой точности позволили качественно изучить геометрию.

Основным выводом общей теории относительности было утверждение, что геометрия нашего мира не эвклидова. Отклонение от законов геометрии Эвклида сказывается прежде всего в том, что тело при отсутствии внешних сил движется не по прямой. Такое отклонение траектории от прямой воспринимается наблюдателем как движение тела под действием какой-то внешней силы, которую привыкли называть силой тяготения. Это значит, что тяготение резко отличается от других сил, которые действуют в природе, электромагнитных и ядерных. Наблюдатель описывает движение тел понятиями геометрии Эвклида и механики Ньютона и любые отклонения от теорем этих наук объясняет наличием новых сил. Сведение сил тяготения к геометрическим свойствам Вселенной позволило решить одну из труднейших проблем естествознания. В связи с этим общую теорию относительности часто называют теорией тяготения.

Продолжение следует.

Автор: А. Я. Смродинский.