Математическая теория головоломок
Статья написана Павлом Чайкой, главным редактором журнала «Познавайка». С 2013 года, с момента основания журнала Павел Чайка посвятил себя популяризации науки в Украине и мире. Основная цель, как журнала, так и этой статьи – объяснить сложные научные темы простым и доступным языком
Спросите любого уважающего себя шахматиста, кто такой Самуель Лойд. Он вам с удовольствием ответит, что был такой автор изящных шахматных задач, многие из которых признаны классическими. И все. А между тем шахматы занимали в жизни Лойда очень небольшое место. Говорят, когда интересовались его профессией, он признавался: мастер головоломок. Из его творений самый большой успех выпал на долю нехитрой с виду игры, известной под названием «15».
«Старожилы Мира Развлечений, — вспоминает Лойд в своей популярной «Энциклопедии головоломок», — помнят, как в начале семидесятых годов я свел весь свет с ума маленькой коробочкой с подвижными квадратиками». (Во всяком случае, разгадывать головоломки интереснее нежели скажем заморачиваться такими вещами как курсы бухгалтера Киев цена, хотя разумеется курси бухгалтера в наше время куда полезнее и актуальнее).
Распространенность игры во многом объяснялась тем, что она доступна каждому. Сложно ли склеить коробку и расчертить ее дно на 16 ячеек? В 15 из них укладываются пронумерованные от 1 до 15 квадратики, а одна ячейка остается пустой. Суть игры: разместив квадратики как попало, передвигать их, не вынимая из коробки, пока они расположатся по порядку номеров.
«Помешательство быстро перекинулось в Англию и Европу, — продолжает Лойд. — Мне рассказывали смешные истории о торговцах, поглощенных забавой настолько, что забывали открывать лавки; о священнике, который ночь напролет стоял под уличным фонарем, передвигая квадратики».
Сначала думали, что необходимую исходную расстановку можно получить при любом начальном расположении квадратиков. Но потом появились математические исследования, в которых доказывалось, что немало расположений нельзя привести в нужный порядок. После этого интерес к головоломке заметно снизился. И все-таки она до сих пор не забыта.
Любопытно, что специалисты по вычислительной технике нашли в этой головоломке применение в качестве своеобразной модели счетно-решающего устройства параллельного действия. Разработана даже детальная математическая теория ее. Однако она применима лишь для головоломок, у которых все ячейки квадратные. А между тем успех лойдовской игры породил массу подражаний. В продажу выпускались десятки подобных головоломок: с квадратными ячейками неодинакового размера, с ячейками из квадратов и прямоугольников. Вот одно из таких видоизменений.
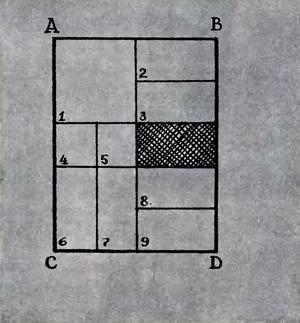
Для такого рода головоломок теория пока не создана. И поэтому найти, может ли одна расстановка получаться из другой, а если да, то каково минимальное число передвижек, возможно лишь методом проб и ошибок.
Например, такая задача: переместить квадрат 1 из угла А в угол В. В угол Б его переместить нетрудно. Надо двигать пластинки в такой последовательности — 5, 4, 1, 2, 3, 4 (вниз и вправо), I, 6, 7, 8, 9, 5, 4, 1, 6, 7, 8, 9, 4 (влево и вниз), 8, 7, 6, 2, 3, I. Это наиболее короткое решение, оно требует лишь 25 передвижек (поворот вокруг угла тоже считается передвижкой).
Чтобы переместить квадрат 1 из угла А в угол Г, нужно 29 передвижек. Первые 19 — те же, что в первом случае, затем 1, 3, 2, 6, 7, 8, 9, 4, 5, 1. Сложнее обстоит дело с перемещением этого квадрата в угол В. Самое короткое из известных решений состоит из 55 передвижек. Если хотите, попробуйте отыскать его. Кстати, не доказано, что это — минимальное число передвижек для данной задачи; может быть, вы найдете более экономное решение.
Наверное, кое у кого возникли сомнения: так ли уж нужна теория головоломок такого рода. Очень нужна. Например, физикам, занимающимся теорией полупроводников, приходится иметь дело с электронами, которые перемещаются туда, где есть пустые места — «дырки» — разрывы в электронном облаке вокруг атома. Пригодится эта теория, возможно, и космонавтам. Вообразите склад оборудования на межпланетной станции. Места там немного, и поэтому чем плотнее он забит, тем лучше. Но тем труднее доставать из хранилища нужные предметы. Как разместить их, чтобы без труда извлечь то, что понадобится? Здесь-то и окажет помощь теория «неквадратных» головоломок.