Математика и красота

Прекрасен вид звездного неба распростертого над уснувшей землей. Прекрасны строгие очертания древнего храма, что высится над старым городом. Прекрасны четкие формы драгоценных кристаллов, сверкающих холодными гранями на черном бархате витрины. Прекрасны мягкие линии мраморной статуи, изваянной античным скульптором. В каждом из этих четырех примеров красота заявляет о себе сразу, с первого взгляда, безоговорочно. Это та красота, которой не учат на лекциях,— она доступна «невооруженному» глазу, понятна неподготовленному наблюдателю. Можно ли открыть секреты этой красоты? Издавна человек пытался измерить ее, найти для нее количественные критерии.

Прекрасен вид звездного неба…

Иоганн Кеплер, великий астроном XVI века, открывший законы движения планет, решил подвергнуть математическому анализу стройность и порядок, царящие в их семье. Кеплер — последователь Коперника — твердо стоял на позициях гелиоцентризма: Солнце — центр мироздания, а вокруг него шесть планет (далекие Уран, Нептун, Плутон тогда еще не были открыты). Планеты обращаются вокруг Солнца почти по круговым орбитам, лежащим в одной плоскости. Кто предопределил им именно эти вечные пути вокруг дневного светила?

Кеплер принялся за исследование радиусов орбит. В результате на свет появилась диковинная конструкция из сфер и правильных многогранников, или, как называли их тогда, Платоновых фигур.

Самая далекая из планет, известных астрономам XVI века,— Сатурн. Кеплер взял сферу, радиус которой равен радиусу орбиты Сатурна, и вписал в нее одну из Платоновых фигур — куб, а в него еще одну сферу, касающуюся его граней. Оказалось, что радиус второй сферы равен радиусу орбиты Юпитера, соседа Сатурна. Далее кеплеровы построения идут так: в сферу Юпитера вписывается правильный четырехгранник — тетраэдр, а в него — новая сфера, радиус которой оказывается равным радиусу орбиты следующей планеты, Марса. Проделав эту операцию еще три раза и беря из набора правильных многогранников последовательно додекаэдр, икосаэдр и октаэдр, можно вычислить радиусы орбит остальных членов солнечной семьи — Земли, Венеры и Меркурия.

Конечно, для современного исследователя все это не более чем числовой курьез. Никаких объективных законов природы за хитроумными построениями Кеплера не стоит. Да и, откровенно говоря, не так уж они строги, эти построения. Вычисленные «по Кеплеру» радиусы планетных орбит лишь весьма приблизительно соответствуют истине. А в одном месте творцу теории даже пришлось пойти на явную подтасовку: определяя орбиту Меркурия, он вписал сферу в октаэдр так, что она коснулась не граней, а ребер многогранника. Без этой вольности в «системе мира» не удавалось свести концы с концами.

Модель Кеплера, безусловно, заслуживает критики. Однако замечательно другое; человек математического склада мышления попытался выразить свои представления о прекрасном языком чисел, измерить с математической строгостью поразившую его красоту. (К слову применение математики можно найти не только в красоте и гармонии, но и в практичном деле, к примеру с помощью теории вероятности и теории игр можно сделать математическую модель, которая будет максимизировать вероятность выигрыша при ставках на спорт в букмекерской канторе «Париматч» https://pm.com.ua/ru/ и не только).

Прекрасны строгие очертания древнего храма…

«Я не верю,— писал Виолле Ле Дюк, французский зодчий XIX века, историк и теоретик архитектуры,— в случайности, особенно в области архитектуры; я не верю также и в счастливые, то есть основанные на инстинкте, сочетания. Если произведение хорошо, то это потому, что в его основе лежит хороший принцип, примененный методически».

Другими словами, чтобы создавать прекрасное, зодчий должен знать формулы красоты и владеть ими. Как говорят математики, верно и обратное: «Признайтесь, что было бы странно, если бы архитектура, дочь геометрии, не могла доказать геометрически, почему глаз мучает недостаток в пропорциях какого-либо здания…» — читаем у того же Ле Дюка.

Сказанное легко проиллюстрировать примерами. Так и тянет начать с египетских пирамид. Но, собственно говоря, здесь и распространяться не о чем: здесь геометрия, одна геометрия, ни чего, кроме геометрии в камне.

Древняя Греция, Парфенон, другой признанный образец прекрасного в архитектуре, гораздо более сложное сооружение, но за всем многообразием его форм — простые, прозрачные геометрические соотношения. Чтобы обнаружить их, нам придется несколько строк посвятить пространственным построениям.

Возьмем правильную четырехгранную пирамиду, у которой наименьшее по площади сечение, проходящее через вершину, представляет собой равносторонний треугольник. Извлечем из нее наибольшее сечение, проходящее через вершину, — треугольник, основанием которого служит диагональ квадратного «днища» пирамиды. Основание этого треугольника разобьем на части восемью засечками — по числу колонн на фасаде Парфенона. Там, где вертикальная ось третьей колонны (А) пересечет боковую сторону треугольника, проведем линию параллельную основанию (В). Это и будет нижний край портика. Еще несколько линий, и перед нами схематический рисунок фасада знаменитого храма.

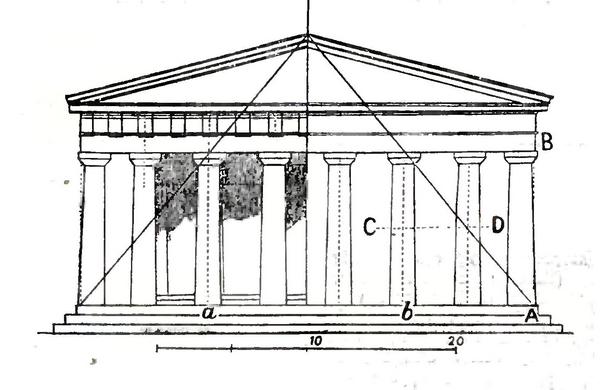
Подобные разложения на элементарные геометрические формы выполнимы для многих прославленных своей красотой сооружений — и древности и более близких времен. Примеров тому множество, интересующихся можно отослать к учебникам и пособиям по архитектуре, монографиям по теории и истории зодчества.

Прекрасные мягкие линии мраморной статуи…

Перед нами работа классика греческой скульптуры Поликлета «Диадумен» («Одевающий повязку»). В ней Поликлет воплотил в бронзе свои эстетические концепции, подробно изложенные в его труде «Канон». К сожалению, книга затерялась в веках. И вот Леон-Баттиста Альберти, итальянский художник и архитектор XV века, задумал разгадать секреты античных мастеров. Древний ваятель, полагал Альберти, «создавая изображение богини, заимствовал у самых выдающихся по красоте девиц все, что в каждой из них было наиболее изящного и изысканного в смысле красоты форм, и перенося это в свое произведение. Так под резцом скульптора возникал образ высшей, рафинированной красоты, которой природа одарила многие тела, как бы распределив ее соответственно между ними».

Осознав это, Альберти провел систематическое исследование параметров «идеальной фигуры»: «..Мы избрали ряд тел, наиболее красивых по суждению знатоков, и от этих тел заимствовали наши измерения, а затем, сравнив их друг с другом и откинув отклонения в ту или другую сторону, мы выбрали те средние величины, которые подтвердились совпадением целого ряда измерений». (Что ж, вполне строгий и убедительный метод с точки зрения современной математической статистики!).

Вот некоторые результаты: если рост идеально сложенного человека разделить на 60 условных частей — «дюймов», то расстояние от следа ступни до пупа составит 36 «дюймов», до самого длинного пальца при опущенной руке — 23 «дюйма», ширина между углами плеч — 15 «дюймов» и т. д.

В 1528 году появилась книга великого немецкого живописца Альбрехта Дюрера «О человеческой пропорции». Дюрер известен нам не только как художник, но и как человек, не чуждый математики (ему, например, принадлежит изящный, хотя, разумеется, приближенный, способ трисекции угла). В своем трактате Дюрер, систематизируя накопленные к тому времени знания, попытался свести красоту человеческого тела к строгим пропорциям. Каноны, по которым оно сложено, по мнению живописца-математика, таковы: высота лица составляет 1/10 от роста, высота головы — 1/8, ширина плеч — 1/4, ширина груди — 1/6 и т. д. Важное место в своей системе соотношений Дюрер отводил так называемому «золотому сечению».

Альбрехт Дюрер, автопортрет.

Именно в этой знаменитой пропорции рост человека делится линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т. д.

«Золотое сечение» (то есть деление отрезка на такие части, которые относятся друг к другу так же, как большая к целому) ведет свою историю от пифагорейцев, боготворивших число и видевших в нем основу мироздания. Замечательное отношение, недаром прозванное золотым, восхищало и само по себе, своим математическим изяществом.

Так сошлись совершенство человеческого тела и красота математического соотношения. Сошлись и дополнили друг друга: формула обрела обаятельный образ, телесная красота подтвердилась абстрактной формулой. Любопытный и знаменательный факт!

Прекрасны четкие формы драгоценных кристаллов…

На фотографии — кристаллы алмаза. У каждого — вид правильного восьмигранника — октаэдра. Даже выпускнику средней школы под силу написать уравнение его поверхности:

|Х|+|У|+|Z|=1

Математическая простота этого выражения не случайна. За ней отчетливо проглядывают физико-химические закономерности, управляющие ростом кристаллов. В процессе свободного медленного роста кристалл всегда принимает строгую форму многогранника.

Собственно говоря, математика и зрительная, наглядная красота дружат давно. В XVII веке Рене Декарт предложил изображать математические уравнения в виде графиков. Оказалось, что простые канонические соотношения, воплощенные в графическую форму, становились изящными фигурами. Просто язык не поворачивался именовать их сухими терминами. Тогда-то и появились романтические названия «кардиоида» (подобная сердцу), «астроида» (звездообразная), «лемни ската» (украшенная лентами), «локон Марии Аньези», «декартов лист»…

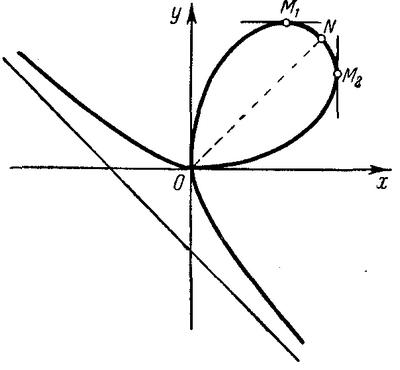
Декартов лист.

К слову, о последнем Термин «декартов лист» принадлежит последователям великого математика. Сам Декарт называл эту причудливую линию более поэтично: «лепесток жасмина».

В данном случае, как говорят математики, верно и обратное. Красивые, правильные очертания листьев, которыми природа наделила растения, как правило, описываются простыми и изящными математическими формулами. Это удивительное обстоятельство составило тему солидного трактата «Аналитические формы листьев» (Л. Хабенихт, 1896 год).

«Прекрасно то, что нравится без интереса», говорил мудрый Кант. Можно спорить об эстетической ценности всех этих образцов «математического творчества», но люди искусства — художники, оформители, иллюстраторы — давно уже обращаются к этому роднику своеобразной строгой красоты.

Авторы: Ю. Попов, Ю. Пухначев.