Занимательная геометрия и проблемы топологии
Статья написана Павлом Чайкой, главным редактором журнала «Познавайка». С 2013 года, с момента основания журнала Павел Чайка посвятил себя популяризации науки в Украине и мире. Основная цель, как журнала, так и этой статьи – объяснить сложные научные темы простым и доступным языком
ГНЕВ БОГОВ
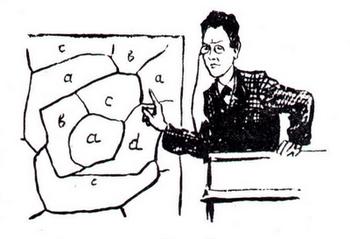
Знаменитый физик Макс Борн в воспоминаниях о своем учителе, известном математике Германе Минковском приводит такой эпизод: Минковский начал рассказ о новой математической дисциплине с изложения так называемой проблемы четырех цветов. При изготовлении географических карт выяснилось, что для закраски любой карты так, чтобы две соседние страны были различны по цвету, необходимо и вполне достаточно иметь четыре цвета.
Он добавил: «К сожалению, это не удалось доказать. Но этим занимались только математики третьего ранга. Я надеюсь это доказательство получить», и здесь он начал свои дедукции… Прошло две-три недели, дело все осложнялось; и даже через три-четыре недели решения не было видно. Когда мы однажды утром собрались в аудитории, разразилась сильная гроза, сверкали молнии, лил дождь. В тот момент, когда Минковский входил в аудиторию, последовал страшный удар грома. Минковский спокойно прошел к кафедре и сказал совершенно серьезно: «Небо гневается на мою дерзость: мое доказательство проблемы четырех цветов тоже неверно». Затем по его лицу пробежала улыбка, и он снова приступил к чтению лекции».
ГЕОМЕТРИЯ РЕЗИНОВОЙ ПЛЕНКИ
Задача, которую безуспешно пытался решить Минковский, кажется, очень простой. Немало и других столь же простых с виду задач рассматривает особая математическая дисциплина — топология. Интересно, что ее возникновение связано с решением «житейской» задачи.
В Кенинсберге было семь мостов, по которым любили прогуливаться городские жители. Рассказывают, что кого-то из них заинтересовал вопрос: как выбрать путь для прогулки, чтобы пройти по всем семи мостам и при этом ни один из них не пересечь дважды. Весть об этой проблеме дошла до знаменитого математика Эйлера, который в это время работал в Петербурге. Эйлер разрешил ее в 1735 году, доказав, что невозможно пройти по всем семи мостам по одному разу.
Однако он сделал больше, чем просто решил задачу о семи мостах. Занимаясь проблемой семи мостов, Эйлер заметил, что у геометрических фигур есть свойства, которые не зависят от их размеров и формы, а зависят только от общего расположения точек и линий. Например, суть задачи о семи мостах не изменится, если мы заменим каждую часть суши точкой, а каждый мост — линией. Тогда мы получим чертеж, который вы видите на рисунке.
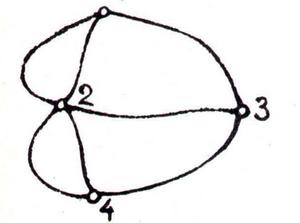
Так и поступил Эйлер, решая задачу. Вот эти-то свойства геометрических фигур, которые не изменяются при их деформациях, и изучает топология.
Утверждения топологии так же верны для фигур, сделанных из резины или нарисованных на резиновой пленке, как и для жестких фигур, с которыми имеет дело обычная геометрия. По этой причине топологию можно образно назвать «геометрией резиновой пленки».
Французский математик Пуанкаре сказал, что утверждения топологии «…остались бы верными, если бы фигуры были скопированы неумелым чертежником, который бы изменил все пропорции и исправил все линии».
Задачи топологического характера возникали еще много веков назад. Согласно старинной легенде, один халиф был так обеспокоен количеством поклонников своей прекрасной дочери, что решил устроить для них испытание. Женихам предлагалась задача: соединить одинаковые цифры на фигурах, которые изображены на рисунке, непересекающимися линиями.
Можно быть уверенным, что если бы халиф не смягчился, его дочь никогда не вышла бы замуж, так как эта задача не может быть решена. Еще в XIX веке физик Кирхгоф понял важность топологических исследований для разрешения проблем, возникающих при изучении разветвленных электрических цепей.
Любопытно, что многие важные явления в физике оказались связанными с такими же расположениями, как и те, что фигурируют в задаче халифа. Вероятно, самой знаменитой нерешенной проблемой после известной теоремы Ферма и, конечно, самой простой с виду является проблема четырех красок, которую пытался решить Минковский.
Парадоксально, что хотя проблема не была решена для карты, нарисованной на плоскости или на поверхности глобуса, она была решена для гораздо более сложных поверхностей. Например, доказано, что семь красок необходимо и достаточно для раскрашивания любой карты, нарисованной на поверхности тора (фигуры, имеющей вид «бублика»)
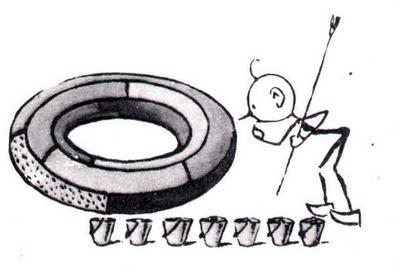
В настоящее время проблемы топологии усиленно разрабатываются математиками многих стран…
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.