Симетрія в науці і мистецтві

Стаття написана Павлом Чайкою, головним редактором журналу «Пізнавайка». З 2013 року з моменту заснування журналу Павло Чайка присвятив себе популяризації науки в Україні та світі. Основна мета як журналу, так і цієї статті – пояснити складні наукові теми простою та доступною мовою.

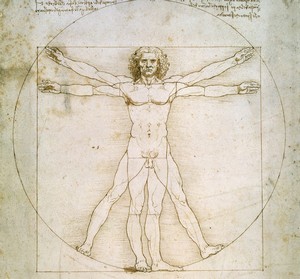
Симетрія – це пропорційність, закономірне взаємне співвідношення частин цілого, притаманне всім творінням природи. Мрія людини – виявити цю закономірність «в чистому вигляді» і втілити в своїй творчості. Але, виявляється, для цього потрібно спочатку уявити собі і саму природу як би «штучно створеною», спеціально «задуманою» і «сконструйованою», інакше нам не вдасться ні пізнати її природну будову, ні навчитися її змінювати та перетворювати. Вивчення симетрії – ключ до вирішення подібного завдання.

Слово «симетрія», успадковане нами від стародавніх греків, буквально означає «відповідність». В античності і середньовіччі симетрію вважали основою гармонії і краси, метою всякої творчості і вінцем її досягнень, символом вищої рівноваги і кінцевої досконалості.

З давніх часів симетрією цікавилися будівельники, лікарі і художники, а в теоретичному плані — математики, які згодом виділили її вивчення в спеціальну гілку своєї науки. Симетрія і сьогодні залишається предметом глибоких досліджень і гарячих дискусій в природознавстві, інженерії, мистецтві та філософії.

Вчені стверджують, що листя квіти, тіла тварин і людей володіють дзеркальною симетрією. На доказ пропонується подумки або на кресленні розсікти ці натуральні тіла навпіл відображаючої площини, або «ідеальним дзеркалом», і переконатися, що спостережуваний патерн виступає як би результатом операції відображення однієї з половин. Збільшення числа уявних дзеркал дає симетрію більш складного вигляду. Відомі й інші різновиди симетрії: поворотна, трансляційна і кольорова.

Намалювавши або вирізавши з паперу вісімку і розташувавши її перед собою вертикально, ми отримаємо якийсь видимий патерн. Якщо трохи повернути вісімку на площині, нахиливши її вправо або вліво, вихідний патерн зміниться, але при повороті на 180 градусів він знову в точності повториться. Фігура вісімки володіє, отже, поворотною симетрією другого порядку. Трилопатевий пропелер «повторює себе» при повороті на 120 градусів (симетрія третього порядку), Хрестовина — на 90 градусів, п’ятипелюсткова квітка жовтця — на 72 градуси (симетрія п’ятого порядку) і т. д. Фігури на зразок вісімки і хрестовини, крім поворотної, мають також і повну дзеркальну симетрію, ламаний хрест — тільки поворотну; складна комбінація обох зустрічається у деяких кристалів.

Трансляційну, або «переносну», симетрію дає малюнок на шпалерах, лінійні орнаменти, мереживні стрічки, паркетні підлоги, черепичні дахи, кахельні печі, мощені плитами мостові, шеренги солдатів, одягнених в уніформу, візерунок на шкурі зебри або змії — взагалі будь-яка повторюваність в просторі через однакову або закономірно зміну відстань.

Всі три різновиди класичної симетрії – відображення, поворот і перенесення — можуть об’єднуватися (так, поворот з трансляцією уздовж осі повороту дає «гвинтові сходи», а поворот з рівномірним розтягуванням радіуса — спіраль), утворюючи велике, але все ж кінцеве число типів патернів, що спостерігаються в живій і неживій природі.

Виклик здоровому глузду

Некласична кольорова симетрія виникає в тих випадках, коли «ідеальне дзеркало» стає до того ж і «кольороактивним», тобто веде до зміни кольору або будь-якого іншого непросторового параметра відбиваного (наприклад, магнітних властивостей атомів). Є й інші варіанти симетрії, що не зводяться до маніпулювання з багатогранниками або будь-якими іншими геометричними фігурами: вони описуються нездійсненними операціями, що існують лише в нашій свідомості і називаються неможливими, будучи, таким чином, абсолютно абстрактними. Але куди ж веде це абстрактне теоретизування? Чи ховається за ним хоч якийсь об’єктивний зміст? Як подібного роду умоглядні конструкції співвідносяться з реальністю?

Ну ось хоча б поняття дзеркальної симетрії: ми ж твердо знаємо, що наші тіла ніякими дзеркалами не розсікаються, і ніякі докази не змусять нас повірити, що колись ми існували в половинному вигляді, маючи тільки одну руку, ногу, пів голови та інше, а потім якийсь дизайнер, рухомий то співчуттям, то ображеним естетичним почуттям, приставив до цих обрубок дзеркальну площину, та й відбив в ній нам відсутні частини заради повноти комплекту…

Спору немає, здоровий глузд нічого схожого в природі не побачить. Всі елементи і операції симетрії створюються і відбуваються в рамках нами ж винайдених моделей — від наочних і простих на зразок кишенькового дзеркальця, що притуляється до сучка або камінчика, і до витонченого апарату математичної теорії груп. Відчуваючи ці моделі будь-якими доступними нам способами, ми пізнаємо їх закономірності, більшість яких аж ніяк не лежить на поверхні і розкривається лише в результаті тривалих експериментів — лабораторних або уявних.

Так ми набагато ефективніше використовуємо до своєї вигоди сили природи, незрівнянно впевненіше заглядаємо в глибини матерії і дізнаємося про наше оточення і про нас самих багато такого, про що ми ніколи і помислити не могли б, не будь у нас настільки вірного і проникливого провідника, як патерни симетрії.

Яскравим свідченням тому – успіхи вивчення структури речовини.

Моделі невидимого

З незапам’ятних часів люди захоплювалися симетрією кристалів, але лише близько трьохсот років тому було встановлено: кути між гранями одного зразка мінералу в точності рівні кутам між відповідними гранями будь-якого іншого зразка того ж мінералу. Суворе повторення характерної симетричності наводило на думку про якийсь єдиний принцип, керуючий їх утворенням, і вселяло впевненість в тому, що аналіз зовнішньої морфології дозволить зрозуміти її причину — невидиму оком внутрішню структуру. Остання ж, згідно з гіпотезою, висунутою в кінці XVIII століття, повинна була бути не чим іншим, як повторенням в тривимірному просторі якихось елементарних цеглинок, що володіють симетрією того кристалографічного класу, до якого належить мінерал.

На початку XX століття експерименти підтвердили наявність в кристалах регулярної атомної решітки: зовнішня симетрія дійсно виявилася наслідком внутрішньої, що поєднує трансляцію з поворотом і відбиттям, тобто утворює гвинтові осі і площини ковзного відбиття (в наші дні завдяки цим знанням налагоджено масове виробництво штучних «дорогоцінних каменів» — від алмазів для абразивних робіт до рубінових стрижнів в лазерах).

Знову той же виклик здоровому глузду: щоб «відкрити» атомну решітку, потрібно було попередньо її винайти, зробити її «дизайн», уявити собі в якості можливої молекулярної структури! Сьогодні це легко: кожен школяр знає, що речовина складається з молекул, а ті будуються з атомів. Але ось звідки це відомо? Окремого атома ніхто ніколи не бачив, та й не в силах побачити. У молекул немає відчутної форми, кольору, смаку, фактури, вони не жорсткі і не м’які, не гладкі і не шорсткі; наші органи чуття не дозволяють нам сприймати їх «поштучно», а наша повсякденна мова абсолютно не годиться для їх опису.

Поняття атома і молекули було введено в науку чисто умоглядно, але потім хіміки, намагаючись уявити самим собі і показати колегам, як саме атоми, за припущенням, комбінуються і утворюють ті чи інші речовини, почали створювати предметні моделі з розфарбованих дерев’яних, металевих і пластмасових куль, що зображують атомні ядра, і стрижнів, що зображують міжатомні зв’язки. На лабораторному столі конструювався видимий і відчутний образ того, що раніше існувало лише перед уявним поглядом хіміка,— тривимірні фігури нагадували знайомі предмети і отримували назви на кшталт «конверта», «пропелера», «крісла» або «човна», у якої були «борти», «ніс», «корми», «бушприт», «флагшток» і т. д.

Розглядаючи потім рукотворні твори власної фантазії, хіміки робили певні висновки про ступінь стійкості даної молекули, про її здатність вступати в реакцію з іншими, тим же способом змодельованими молекулами, утворювати нові сполуки і т. д. Потім вони ставили експерименти з реальними речовинами — проводили реакції, вимірювали і зважували, робили рентгенокристаллограмми і напружено вдивлялися в чергування темних і світлих плям на знімках, піддаючи їх все більш витонченій і абстрактній математичній інтерпретації і намагаючись уявити собі можливі траєкторії ікс-променів, що дали при падінні на фотопластинку той чи інший патерн, а потім — характер перешкод, змусили ці промені скривитися при проходженні через речовину саме таким чином.

Отримавши результати, що в чомусь збігаються, а в чомусь розходяться з передбаченими, хіміки, які працювали все в більш тісній співдружності з кристалографами і математиками, ускладнювали і вдосконалювали свої моделі, додаючи нові кулі і стрижні, змінюючи їх конфігурацію, відстані і так далі, прагнучи домогтися більш адекватного відображення істинної, тобто відповідної досліду молекулярної структури. Дехто з таких вчених (іноді навіть вельми великих) настільки захоплювався цим заняттям, що починав необережно приймати свої творіння за дійсний устрій речовини, і тоді його наукова творчість відразу ж гальмувалася, а то і фатально зупинялася: адже в реальних молекулах немає рішуче нічого схожого на кулі, стрижні і будь-які інші доступні нашому сприйняттю предмети.

У чому ж полягає евристична міць цих вигадливих симетричних конструкцій, що нагадують абстрактні скульптури, і чим керується дослідник, здійснюючи черговий пробний крок на шляху конструювання того чи іншого патерну?

Вдала модель молекули розділяє зі своїм оригіналом одну важливу особливість: «властивості симетрії моделі в точності збігаються з властивостями симетрії молекули. Спільність симетрії моделі і молекули служить дороговказною ниткою для уяви хіміка. Побудувавши кілька різних моделей однієї і тієї ж молекули, він може потім поцікавитися геометричними властивостями, загальними для всіх моделей. Саме цими властивостями може володіти і сама молекула, і вона дійсно володіє загальними властивостями симетрії моделей».

Симетрія залишається надійним орієнтиром вчених і при переході від мікро – до макромасштабів. Вона виступає невід’ємною частиною мови і методів сементологів, які вивчають осадові породи, палеонтологів і геоморфологів, які створюють моделі гідро-, біо – і тектонічних явищ і процесів найдавніших епох, а також геофізиків, моделюючих внутрішню будову Землі за паттернами відображення сейсмічних хвиль.

У цьому випадку дослідники з якоїсь однієї частини явища або процесу реконструюють весь процес, в тому числі відтворюють і приховані від очей його закономірності. Ряд новітніх досліджень світового океану і відродження забутої було теорії дрейфу материків виходять з трактування підводних хребтів в якості своєрідних площин симетрії, оскільки, наприклад, розташування і вік згаслих вулканів по одну сторону хребта виявляється «дзеркальним відображенням» таких же структур по іншу його сторону.

У всіх подібних випадках симетричний дизайн відповідних моделей речовини, будь то на атомно-молекулярному або глобально-геологічному рівні, дозволяє представити в зримих предметних образах те, що в своєму природному бутті або зовсім недоступно прямому спостереженню, або затулено від нас якимись випадковими рисами. Це рішуче підриває поширену думку про торжество кількісних методів і повне вигнання образних уявлень з сьогоднішньої науки. І те й інше продовжує бути одно важливим: чим складніше проблеми, що постають перед сучасним дослідником, чим менше вони даються йому в безпосередньо відчутній емпірії, чим абстрактніше робиться застосовуваний для їх аналізу математичний апарат, тим більша потреба в засобах чуттєво-наочного відображення досліджуваної ним реальності.

«Було б дуже корисно, – підсумовує Джордж Флек — якби хто-небудь з майбутніх хіміків зайнявся розробкою яскравої і в той же час точної мови, що дозволяє говорити про молекули, черпаючи аналогії з мистецтва та інших областей творчої діяльності людини, в яких знаходять застосування принципи симетрії і теорія груп». Додамо, що подібного роду мови були б надзвичайно корисні і в багатьох інших природно-наукових і суспільних дисциплінах, що мають справу з об’єктами, або принципово невидимими, або не доступними для огляду цілком через свою множинність.

Але щоб надихатися і керуватися симетрією при створенні моделей і аналізі досліджуваних фактів, потрібно перш за все вміти знаходити її в нескінченній строкатості емпіричної дійсності. Кращий же спосіб придбати таке вміння – впритул познайомитися з теорією симетрії і в математиці, і з її практикою в мистецтві. Ті, хто звик вважати першу чимось сухим і чужим будь-якої естетики, а другу — максимально далеким і навіть ворожим будь-яким математичним залежностям, будуть чимало здивовані не тільки їх кровною спорідненістю, але і тим, наскільки тісно абстрактні висновки переплітаються в даному випадку з конкретними художніми експериментами.

За словами Марджорі Сенешаль, «теорія візерунків (патернів) бере початок в математиці більшості народів стародавнього світу. Витонченість форм і ліній, яким відрізняється мистецтво орнаменту древніх, наводить на думку про те, що художники того часу були обізнані про абстрактну проблему покриття площини конгруентними і різними багатокутниками».

Як зауважив у своїй книзі «симетрія» Герман Вейль, «зразки всіх сімнадцяти груп симетрії виявлені серед декоративних візерунків давнини, особливо серед єгипетських орнаментів… Мистецтво містить в неявному вигляді найбільш давню частину відомої нам вищої математики…» Знову якесь невловиме парадоксальне перевертання причин і наслідків! Як же все-таки йде справа: чи випереджають художники вчених у відкритті (винаході) законів симетрії або, навпаки, спираються в своїй творчості на знання, здобуті наукою?

Подібна постановка питання тут, однак, недоречна. Перед нами — зустрічна взаємодія, невпинне взаємне відбивання, ціннісна симетрія двох одно активних полюсів культури. Одне немислимо без іншого. Наприклад, розробка рівномірно темперованого звукоряду, що склав, починаючи з XVIII століття, тональну базу всієї «вченої» європейської музики, мотивувалася прагненням внести певного роду симетрію в її гармонійні структури і здійснювалася за участю видних математиків та фізиків. Але не менш показово те, що великий астроном Йоганн Кеплер поставив за мету свого життя створення «гармонії світу» — математичної моделі руху небесних тіл, що зв’язує дослідні дані системою числових відносин, прийнятих в музичній естетиці його часу!

Автор: Л. Переверзєв.