Для тих, хто не любить математику. Або як вивернути сферу навиворіт.

Великий математик Давид Гільберт сказав одного разу, що математичну теорію можна вважати досконалою лише тоді, коли її вдається викласти першому зустрічному. Послідовники Гільберта приходять в повний відчай, намагаючись жити за цим рецептом. Математика все більше спеціалізується, і зараз вченому математику часом коштує чималих зусиль навіть своїм колегам пояснити суть розв’язуваних ним завдань. Однак час від часу дослідження в провідних і, здавалося б, недоступних розумінню галузях цієї науки призводять до відкриття, яке цікаво для непрофесіонала і в той же час може бути пояснено без надмірного спрощення. Вражаючий приклад цього – теорема Стефена Смейла про так звані регулярні відображення сфери, опубліковані в 1959 р.

Область, в якій тоді працював Смейл, – диференціальна топологія – одна з найбільш абстрактних галузей сучасної математики. Тим дивніше, що все-таки вдалося придумати наочне пояснення одному з найбільш вражаючих наслідків з теореми Смейла. А саме, можна продемонструвати, як треба вивертати сферу навиворіт.

У звичному сенсі це, звичайно, неможливо: сферу обов’язково довелося б розірвати. Але в диференціальній топології дозволяється – подумки, зрозуміло, – протягати поверхню крізь саму себе – такі «правила гри» у цій науці. Але тоді відразу впадає в очі просте рішення.

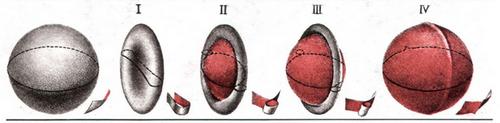
Треба стискати протилежні сторони до центру, поки вони не пройдуть один крізь одного (I). Внутрішня, пофарбована поверхня (II) проступає з двох протилежних країв. Продовжимо цей процес «витягування» внутрішньої поверхні до тих пір, поки колечко, утворене частиною зовнішньої поверхні (II), зовсім не зникне. Нажаль, при цьому процесі колечко утворює тугу петлю (III), яку доводиться затягнути. У результаті виходить рубець (IV), а це не задовольняє диференціальної топології, тому що вона розглядає тільки так звані «гладкі поверхні», у яких немає ніяких кутів і зламів.

Отже, завдання полягає в тому, щоб вивернути навиворіт сферу таким чином, щоб, позбавляючись від колечка, не отримати рубця. І тут інтуїція знову підказує, що завдання нерозв’язне. Коли Смейл вперше оголосив, що він може довести існування рішення, то йому ніхто не повірив. Але інтуїція була неправа: у доказі Смейла не знайшлося жодної логічної помилки. Математики переконалися, що теоретично можливо простежити доказ крок за кроком і знайти явний опис деформації, вивертаючої сферу. Але це було настільки складно, що здавалося безнадійною справою. Протягом деякого часу після відкриття Смейла було відомо, що в принципі можна вивернути навиворіт сферу без рубця, але ніхто не мав ні найменшого уявлення, як це здійснити.

Але, врешті-решт, математики з цим завданням впоралися. Як – зрозумієте, розглянувши малюнки. Вони цікаві.

Хоча доказ Смейла не складався з одних малюнків. Цікаво, що в його роботі їх взагалі немає – занадто вже й складні ті фігури, які в неявному вигляді містяться в його абстрактному аналітичному апараті. Їх не вдалося б зобразити самому винахідливому художнику – фантазія математиків разюча. Але, мабуть, ще більш разюча їх здатність передавати один одному найскладніші ідеї, не вдаючись до малюнків. Історія з вивертанням сфери – яскраве тому свідчення. Вона стала відомою широкій публіці завдяки французькому топологу Рене Тома, який дізнався про неї від свого колеги Бернара Морена, а той, у свою чергу, – від американця Арнольда Шапіро, винахідника цієї «виворотки». Ось це особливо цікаво, якщо врахувати, що Бернар Морен сліпий.

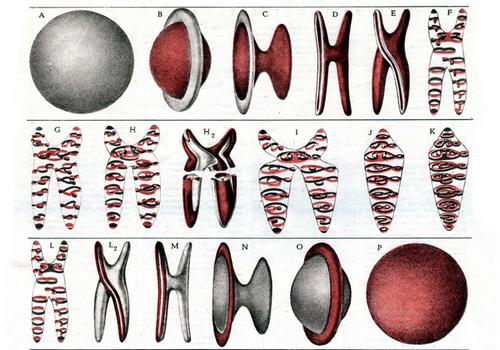
На цих картинках показано, як можна вивернути сферу навиворіт, і при цьому не порушити вимог диференціальної топології. Спочатку треба зблизити протилежні сторони сірої сфери (А), продавлюючи їх одна крізь одну. Тоді з двох сторін проступає пофарбована поверхня (В). Потім треба розтягнути один із забарвлених шматків (С) таким чином, щоб отримати поверхню, що нагадує сідло на двох «ногах» (О). Ці дві ноги перекручують проти годинникової стрілки і отримують поверхню Е. Вона ж показана знову (Р) «у розрізі» за допомогою стрічок, які, як і в «сфері з рубцем», зображують поперечні перетини на десяти різних рівнях.

Далі немає сенсу зображати отримувані на кожному етапі поверхні – аж надто вони складні. Але можна, якщо завгодно, розглянути стрічки на всіх 10 рівнях і подумки домалювати. Один етап (H2) ми все-таки вирішили показати – просто, щоб можна було собі уявити, який тип фігур, що утворюються. Поверхня G з’являється після стиснення і обертання на 90 ° сідла поверхні Р.

Ще кілька кроків. А саме: між етапами I і J дві однакові за формою ноги проходять одна крізь одну. У кожного перетину поверхні на етапі J є два сірі боки, звернені один до одного. Між етапами J і К внутрішній шар розширюється, а зовнішній стискається; виходить поверхня К – абсолютно така ж, як J, але тільки кольори помінялися місцями.

Далі всі дії йдуть в «зворотному порядку». Ви можете скласти про них уявлення, розглядаючи картинки I, Н, С і т. д. Треба тільки міняти місцями кольори стрічок на кожній картинці. Закінчення цього другого ряду картинок ми наводимо. Поверхня L відповідає поверхні F, L2 – Е, і т. п.

Пофарбована сфера (поверхня Р) відповідає сірій сфері (поверхні А). Отже, деформація виконана, і рубця немає. Сама можливість цього трюку була вперше доведена С. Смейлом. А всі послідовні етапи деформації придумав А. Шапіро.

Автор: Д. Рыжков.