Момент інерції у фізиці

Що таке інерція?

Інерція у фізиці – здатність тіл певний час зберігати стан руху при відсутності дії зовнішніх сил. Втім, поняття інерції має часте застосування не тільки у фізиці, але і в нашому повсякденному житті. Так зазвичай «інертною» називають людину, яка зовсім не проявляє ніякої ініціативи, робить тільки те, що їй скажуть інші, і робить це вкрай повільно, без будь-якого ентузіазму. «Рухається по інерції», – говоримо ми, коли хочемо підкреслити, що щось робиться без будь-якого сенсу, а просто тому, що так було заведено колись або в силу напрацьованої роками звички. І якщо з поняттям інерції все більш-менш зрозуміло, завдяки таким ось життєвим прикладам, то термін “момент інерції” вимагає більш детального пояснення, чим ми і займемося в нашій статті.

Визначення

Зі шкільної програми з фізики ми прекрасно знаємо, що маса тіла є мірою його інертності. Наприклад, якщо в супермаркеті сильно штовхнути два візки, один з яких буде порожній, а другий навантажений різними товарами, то згодом зупинити буде важче візок, навантажений товарами в силу його більшої маси. Іншими словами, чим більша маса тіла, тим більше на нього вплив інерції і тим більше потрібно сил, щоб змінити рух такого важкого тіла.

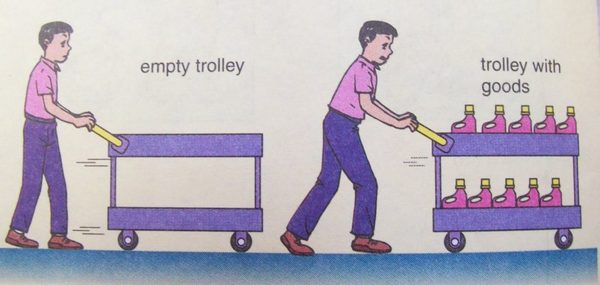
У наведеному прикладі візок рухається по прямій лінії, тобто іншими словами робить поступальний рух. І якщо при поступальному русі якогось тіла його маса є мірою його інерції, то при обертальному русі тіла навколо своєї осі мірою його інерції буде величина, яка власне і називається – момент інерції.

Момент інерції – скалярна фізична величина, міра інертності тіла при його обертанні навколо осі. Зазвичай позначається буквою J і вимірюється в кілограмах, помножених на квадратний метр. Таке академічне визначення того, що таке момент інерції.

Формула

Як розрахувати точне значення моменту інерції? Для цього є загальна формула, що допомагає фізикам визначати момент інерції будь-якого тіла. Якщо тіло розбити на нескінченно маленькі шматочки з масою dm, то момент інерції буде рівним сумі добутку цих елементарних мас на квадрат відстані до осі обертання. Формула матиме такий вигляд:

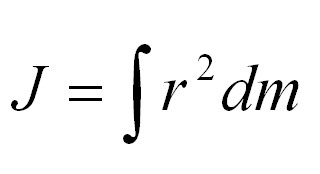
J – момент інерції, r – відстань до осі обертання.

Для матеріальної точки маси m, яка обертається навколо осі на відстані r, дана формула матиме такий вигляд:

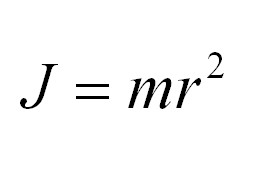
Теорема Гюйгенса – Штейнера

Говорячи про момент інерції неможливо не згадати про теорему двох математиків Гюйгенса і Штейнера, які дали формулювання визначення характеристики паралельних осей.

Теорема Гюйгенса-Штейнера говорить: момент інерції тіла щодо довільної осі дорівнює сумі моменту інерції тіла щодо осі, що проходить через центр мас паралельно довільній осі і добутку маси тіла на квадрат відстані між осями.

Якщо записати вищесказане математичною формулою, то вийде наступне:

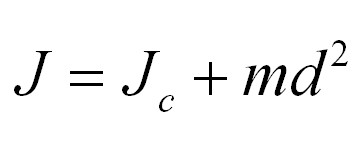
Де d – відстань між осями

Ця теорема значно полегшує вирішення багатьох фізичних завдань, пов’язаних з інерцією. Скажімо, у Вас є об’єкт довільної форми, відцентрова сила якого відома. За допомогою формули Штейнера можна обчислити момент інерції тіла щодо будь-якої осі паралельної лінії, яка проходить через середину фігури.

Приклади найпростіших об’єктів

Незважаючи на зовнішню простоту, обчислення моментів інерції для різних предметів передбачає знання інтегралів, цих важливих інструментів вищої математики. Для спрощення задачі створена таблиця з обчисленнями інерції для простих геометричних фігур: кола, квадрата, циліндра і т. д.

Так виглядають математичні розрахунки обчислення моментів інерції для кола і кільця.

Аналогічним чином буде розраховуватися момент інерції циліндра.

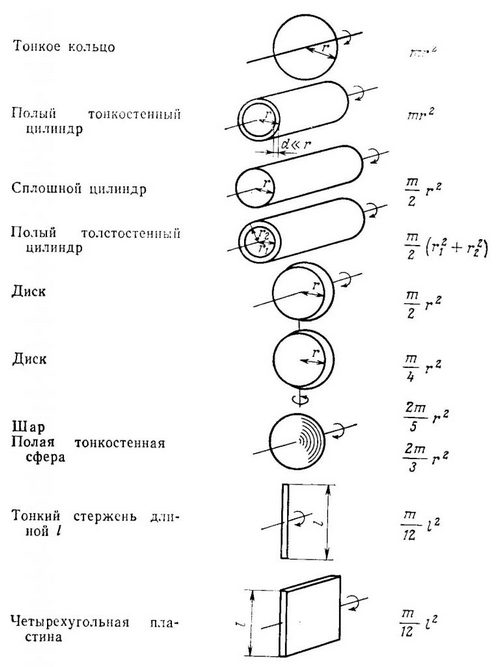
Пропонуємо вашій увазі більш детальну таблицю з формулами для розрахунку моменту інерції для основних геометричних фігур: кулі, сфери, диска, циліндрів, і т. д.

Рекомендована література та корисні посилання

• Тарг С. М. Момент інерції // Фізична енциклопедія / Гл. ред. А. М. Прохоров. — М: Велика Російська енциклопедія, 1992. — Т. 3. — С. 206-207. — 672 с.-48 000 прим. – ISBN 5-85270-019-3.
• Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. – P. 77-84. — DOI:10.1126/science.286.5437.77. — PMID 10506564.
• Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.)рос. : journal. — 2012. — Vol. 117. — DOI:10.1029/2012JE004161.
• Галкін І. М. позаземна сейсмологія. — М: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля і Всесвіт). – 15 000 прим. – ISBN 502005951X.
• Матвєєв. А. Н. Механіка і теорія відносності. М.: Вища школа, 1986. (3-е изд. М.: онікс 21 століття: світ і освіта, 2003. — 432с.)
• Трофімова Т. І. Курс фізики. — 7-е изд. — М: Вища школа, 2001. — 542 с.
• Алешкевич В. А., Деденко Л. Г., Караваєв В. А. Механіка твердого тіла. Виклади. Видавництво Фізичного факультету МДУ, 1997.
• Павленко Ю. Г. лекції з теоретичної механіки. М.: ФИЗМАТЛИТ, 2002. — 392с.
• Яворський Б. М., Детлаф А. А. Фізика для школярів старших класів і вступників у вузи: навчальний посібник — М: Дрофа, 2002, 800с. ISBN 5-7107-5956-3

Автор: Павло Чайка, головний редактор журналу Пізнавайка

При написанні статті намагався зробити її максимально цікавою, корисною та якісною. Буду вдячний за будь-який зворотний зв'язок та конструктивну критику у вигляді коментарів до статті. Також Ваше побажання/питання/пропозицію можете написати на мою пошту pavelchaika1983@gmail.com або у Фейсбук.

Сторінка про автора

Ця стаття доступна англійською мовою – Moment of Inertia.