Під знаком інтеграла – математична п’єса

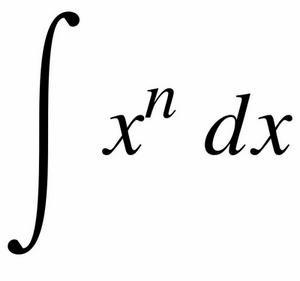
Математика зараз просочує всі розділи знань. Вже і лінгвісту, і фізіологу, і історику не терпиться дістати її в свій арсенал. Але знаходяться скептики, які не схильні крокувати в ногу. Скептицизм, дух сумніву — життєвий сік науки. Без нього навіть найперспективніший і яскравий науковий напрямок швидко вироджується в затхлу дрібну водойму, де всі по черзі віддають хвалу один одному, намагаючись не помічати, що життя мчить незалежно від них. Жовчний і єретичний скептик не милує нікого і нічого, навіть математики дістається від нього. Найлегше раз і назавжди визнати в скептику заздрісного невігласа і більше не опускати себе суперечкою з ним. Куди важче і корисніше прийняти, що навіть самий підступний і злостивий скептик науці корисніше миролюбного легкодума. Тому не будемо позбавляти скептика слова, навіть якщо мова його перестане пестити слух.

Місце дії – буфет науково-дослідного інституту. Зліва – кавоварка з чергою, праворуч на стіні — графік залежності тривалості життя від числа викурених сигарет. На передньому плані сидять за столиком Математик і Скептик.

МАТЕМАТИК (помішуючи каву): – ти вже читав? Сенсація! Вдалося довести нерозв’язність проблеми Дьюї-Ізмара.

СКЕПТИК (закурюючи): – не читав і читати не буду. По-перше, я там нічого не зрозумію – це, здається, входило в наміри автора. А по-друге, мені це не потрібно: наука може розвиватися і без цього доказу. Хіба що якийсь сноб пошлеться на цю роботу, щоб проявити ерудицію. Скільки їх зараз розплодилося! Ось тобі докторська дисертація, щойно затверджена ВАКом; автор явно не в ладах з елементарною алгеброю, але це не заважає йому, поминаючи всіх математичних святих, хоробро будувати наукові теорії і уявляти себе десь поруч з Вінером. А хто його союзник? Псевдоматематична фразеологія, якою начинена робота і яка справляє враження на непосвячених.

МАТЕМАТИК: – постривай, причому тут математика? Мені теж відомі такі випадки, але повір, саме завдяки математиці будь-який фахівець може тут же викрити таку саморобку.

СКЕПТИК: – але ти ж не викрив.

МАТЕМАТИК (неуважно): – ось ще! Чому мені розбирати провини якогось… Є чимало прикладів справді наукового використання досягнень математики.

СКЕПТИК (іронічно): – Ось як? Приведи.

МАТЕМАТИК (невпевнено): – Ну, наприклад, розрахунок руху космічного корабля.

СКЕПТИК: – давай домовимося вважати математикою лише те, що вироблено останньою за століття. Що стосується траєкторії матеріальної точки, то її в принципі вміли розраховувати ще в XVIII столітті. Правда, зараз це роблять набагато простіше і швидше за допомогою комп’ютера, але це досягнення не математики, а електроніки.

МАТЕМАТИК (єхидно): – а як щодо аналізу міцності корпусу космічного корабля? Вже він-то, цей розрахунок, Ейлеру був безумовно не під силу.

СКЕПТИК: – на жаль, і в цьому завданні ми недалеко пішли від старого Ейлера. Інженери, що проектують складні літальні апарати, подібно кораблебудівникам часів Ейлера, куди більше довіряють досвіду, ніж розрахунку. У розрахунку конструкцій на міцність ви, математики, трохи дали практиці. Ось що пише американський інженер Пармлі (Скептик розкриває книгу, що лежить поруч з попільничкою і читає): «Мистецтво фахівця з розрахунку конструкцій полягає в тому, щоб досліджувати тверде тіло, конфігурація якого нам в точності не відома, на дію навантажень, про які ми не маємо уявлення, з матеріалів, фізичні властивості яких для нас загадка, причому зробити це так, щоб у широкої публіки не зародилося ніяких сумнівів». І математика допомагає в цьому мистецтві, бо позбавляє розрахунок від загрози перевірки.

МАТЕМАТИК: – Ну, це ти хватив: теорія пружності – один з головних додатків математики, яким математика по праву пишається. Скільки глибоких і тонких побудов зроблено, скажімо, щоб описати розподіл напруг поблизу кінця тріщини. Або, скажімо…

СКЕПТИК: – ось-ось, кінця тріщини… Тобто для найпростішої модельної задачі. А тріщина зазвичай буває не одна, тріщини переплітаються між собою і проходять по неоднорідному матеріалу, та ще й розвиваються в часі… Звичайно, існують теорії, які враховують ці ефекти. Але ось парадокс – в таких теоріях використовуються самі елементарні математичні засоби, що майже вміщаються в шкільний курс. А де додатки математичної думки останнього часу?

МАТЕМАТИК: – я міг би посперечатися з тобою, довести, що останні досягнення математики використовуються в теорії руйнування, але краще я оберу інший шлях. До речі, він покаже, наскільки різноманітні додатки математики. Візьмемо зовсім інший приклад: економіка. Наприклад, лінійне програмування, що з’явилося якихось сорок років тому, здатне дати оптимальний розподіл ресурсів в масштабах великих економічних систем.

СКЕПТИК: – Якщо я почну копати цю область, то доведеться витягнути на світ чимало соромливих недомовок. Справа в тому, що нам поки не ясно, що розуміти під оптимальним розподілом. Тобто невідомо, що ми шукаємо. А це, погодься, дещо знижує радість від знахідки. Є до лінійного програмування й інші претензії. Наприклад, та, що для вирішення завдань економіки з його допомогою потрібні буквально полчища цифр, гори вхідної інформації. І жодну з них ми не вміємо встановити в точності. А метод розв’язання задачі влаштований так, ніби кожне з чисел у задачі відоме нам з абсолютною точністю. Так що на практиці економісти досі користуються найпримітивнішою схемою: підраховують вартості двох варіантів і вибирають, який дешевше.

МАТЕМАТИК: – я можу навести тобі приклади конкретного виробничого ефекту, отриманого за допомогою лінійного програмування. Наприклад, в задачах розкрою матеріалів. Просто вже пройшла пора повального захоплення лінійним програмуванням. Крім того, були розроблені нові, більш ефективні в деяких випадках засоби. Скажімо, метод випадкового пошуку. Але це не дає тобі приводу для зловтіхи: процес оновлення наукових методів — це природний процес. І він анітрохи не кидає тіні на науку.

СКЕПТИК: – щось недобре виходить: з’явився новий науковий метод, який змінюється ще більш новим. Старий кумир повалений, публіка аплодує новому і покладає на нього надії. «Вже він-то не підведе!» Тим часом сумний досвід міг би навчити більш тверезої оцінки.

МАТЕМАТИК: — слухаючи тебе, запідозриш, що тисячі автоматизованих систем у всьому світі – це блеф. Що не ці системи керують виробництвом, розраховують і друкують кошториси, підраховують підсумки виборів і спортивних змагань, планують капітальні вкладення, виробляють банківські операції та інше, та інше.

СПЕКТИК: — Чому ж? Не блеф! Все це дійсно робиться. Але розберемо по порядку, почавши зі спортивних змагань. Невелика мудрість скласти очки і поділити їх на число суддів. Просто машини роблять це миттєво і точно, але математика тут ні при чому. Кошториси? Це вибірка нормативів, множення і додавання; але головне — вибірка нормативів — до математики не має стосунку. Банківські операції? Трохи складніше: до додавання і віднімання додається розрахунок складних відсотків. А якщо в АСУ і доводиться що-небудь розрахувати серйозніше, наприклад, знайти розклад з мінімальними простоями, то знову-таки роблять це без всяких там математичних премудростей, а за допомогою найпростіших і нестрогих, так званих «евристичних» правил і алгоритмів. Правил, які ви, математики, не погоджуєтеся навіть допустити в передпокій математичних знань.

МАТЕМАТИК (дратуючись): – ти, як водиться серед критиканів, неабияк відстав від життя: математика вже займається вивченням евристики, нестрогих алгоритмів, нечітких множин, штучним розумом та іншими речами, які ти сміливо виніс за її рамки.

СКЕПТИК: – ось саме, вже займається. Ти не зміг обійтися без цього слова. Після того, як ці прийоми рахунку були запропоновані практиками, багаторазово використані і дали ефект, математика береться за те, щоб вибудувати з них ланцюжки теорем, навести академічний глянець і викласти на тій говірці, яку ви називаєте строгою математичною мовою. Математики зі своєю пристрастю до формалізації, таким чином, користуються здоровим глуздом, властивим фізикам та інженерам, хімікам та економістам. Пошлюсь на приклади тільки з однієї області – варіаційних методів для вирішення крайових задач, які служили головним інструментом для обробки диференціальних рівнянь до появи комп’ютерів.

Головні методи в цій галузі – методи Тимошенко, Бубнова-Галеркіна, Треффтца — чисто інженерні методи. Їх винайшли інженери, а лише потім математики почали їх обґрунтовувати. До речі, знаменно, що до моменту повного і всебічного обґрунтування ці методи вже застаріли і змінилися іншими, які «краще лягають на машини». Так що період активного використання цих методів фактично пройшов без участі математиків. Здається, те ж саме чекає і найбільш популярний зараз серед інженерів метод вирішення крайових завдань – метод кінцевих елементів.

МАТЕМАТИК: – і тут у тебе пересмикування. У розробці варіаційних методів велику роль зіграли математики, наприклад, Канторович і Курант. Крім того, твоє протиставлення інженерів і математиків взагалі неправомірно: інженери, яких ти назвав, блискуче, на рівні кращих математиків володіли всіма математичними методами. Для багатьох з них взагалі неможливо сказати, хто він, інженер або математик.

СКЕПТИК: – володіти-то вони володіли, але все ж на першому місці для них стояло вирішення завдання, і вони не утруднювали себе обгрунтуванням методів. Так само чинять і сучасні прикладники. І навпаки, математики, яких ти назвав, і ще кілька імен представляються мені винятками. У той час як більшість математиків виснажують свої плоть і дух безглуздими вправами у формальній логіці або зашифровують з незрозумілого доступні всім побудови фізиків і інженерів.

МАТЕМАТИК: – найбільші математики ніколи не цуралися додатків. Візьми такого гіганта, як Гільберт. У свій знаменитий перелік найважливіших математичних задач він включив проблему № 6: «Аксіоматизувати ті фізичні науки, в яких важливу роль відіграє математика». Це означає, що механіка і теорія електрики, подібно геометрії, повинні постати у вигляді ряду умовиводів, що струнко випливають з декількох аксіом. Гільберт і сам доклав чимало сил до вирішення цієї проблеми, хоча дехто досадував на таке відволікання.

СКЕПТИК: – не забудь додати, що спроба Гільберта закінчилася невдачею, надалі більшість фізиків відкинули аксіоматичний підхід. Таким чином, великий Гільберт своїм екскурсом за рамки математики лише поповнив плеяду теоретиків, які, за образним висловом М. В. Ломоносова, «натуральну науку більше затьмарили, ніж світла їй надали».

МАТЕМАТИК: – подібно багатьом невігласам, ти самовпевнений. Тобі здається позбавленим сенсу все те, чого ти не розумієш. Ти не розумієш так званої «чистої математики» і готовий таврувати її тільки за це. Але згадай, що вважають авторитети: кожен нетривіальний математичний факт адекватний якомусь матеріальному явищу, служить його формальним описом. Не біда, якщо ми не можемо відразу ж знайти фізичне або суспільне явище, що відповідає будь-якій теоремі. Треба мати терпіння і чекати — воно знайдеться. Згадай, наприклад, теорію узагальнених функцій. Вона представлялася абстрактною. А тим часом у квантовій механіці знайшовся об’єкт, який такою функцією описується.

Якийсь час представлялася абстрактною топологія — це навіть відобразили в художній літературі. А потім з’ясувалося, що в багатьох випадках при аналізі електричних мереж без неї — нікуди. Теорія груп – порожня Абстракція, ніякого зв’язку зі світом речей. А що б тепер без неї робили фахівці з кристалографії? Так що основна схема відкриття зараз в прикладних науках така: математик будує абстрактну теорію, а грамотний прикладник, а то і математик, застосовує її.

СКЕПТИК: – і тут ти не правий. Узагальнені функції фізики стали застосовувати задовго до того, як математики наклали на них лак. Те ж сталося і з топологією. А математики потім розвинули ці теорії, як сказав один видатний механік, «далеко за рамки необхідності» вже у вигляді вправи в своєму дивному і малодоступному спорті. Ні, є прості прийоми рахунку, придумані прикладниками, і окремо існує якийсь заум, який носить чисто декоративний характер. Саме заради нього, а не заради справи, звертається прикладник до математики і просить: «слухай, мені тут треба математики підкинути. Сам знаєш, зараз це люблять…»

МАТЕМАТИК: – циніки є в будь-якій галузі науки. Але з цього зовсім нічого не випливає. Між іншим, математика – невиграшне поле діяльності для оковтирателя…

СКЕПТИК: – Погано ти їх знаєш! Вони давно засвоїли, що найвірніша справа — обрушити лавину важких формул, а найбільш обережні не дають додатково до цих формул розшифровки позначень. Пам’ятаєш, як всюди обговорювали «машину Діна». У мало зрозумілому американському патенті з формулами дехто побачив ні багато ні мало, як спростування третього закону Ньютона. Чомусь ніхто не звернув уваги на те, що автор не знайомий із загальноприйнятим позначенням похідної. Але ж цього було достатньо, щоб припинити безплідну дискусію на самому початку. Обійдися Дін без формул – йому б ніхто не повірив. Але формули, над якими впору було посміятися школяреві, справили гіпнотизуючу дію.

МАТЕМАТИК: – Ти сам собі суперечиш: мабуть, Діна викрив перший же математик, заглянувши в патент. Але ти стверджуєш, що вчений може спокійнісінько творити, не обтяжуючи себе вивченням математики, що вона марна для дослідника. Але навіть ти, настільки мало знайомий з цією наукою, не станеш же заперечувати користь статистичного аналізу? (Показує на криву тривалості життя.) Хіба статистика не дозволяє зробити корисні висновки про здоров’я людини? Про шкоду землетрусів? Про якість продукції?

СКЕПТИК: – дозволяє, якби не «але»… По-перше, статистика займається оцінкою гіпотез, які повинні бути правильно складені. Ось перед тобою графік, ти думаєш, він говорить про шкоду тютюну? (Закурює.)

МАТЕМАТИК: – безсумнівно. Крива, яку ти бачиш, відображає велику кількість фактів. Якщо хочеш продовжити життя, кидай курити.

СКЕПТИК: – тоді слухай. Тобі траплялося застуджуватися?

МАТЕМАТИК: – траплялося. Ну то що?

СКЕПТИК: – ти при цьому кашляв?

МАТЕМАТИК: – так.

СКЕПТИК: – а міг би стриматися і не кашляти?

МАТЕМАТИК: – іноді, мабуть, міг би.

СКЕПТИК: – Так ось тобі спосіб лікування: старайся не кашляти, і все тут.

МАТЕМАТИК: – яка нісенітниця! Адже кашель – це не причина хвороби, це її симптом.

СКЕПТИК: – а чому ж тоді кількість викурених сигарет ти оголошуєш не симптомом, а причиною? Бути може, люди певного фізіологічного складу схильні одночасно як до паління, так і до раку. Тоді відмова їх від куріння покаже лише, що насправді вони мало схильні як до куріння, так і до раку, якщо змогли цю відмову зробити. Зауваж, я нічого не стверджую, я лише показую, як можна поставити під сумнів всякий висновок, заснований на статистиці.

Втім, ми даремно так довго затрималися на цій сумній темі. Але і щодо землетрусів, і з якістю продукції справа йде не краще. Всі запропоновані підходи вразливі до критики. Час від часу черговий імовірнісний підхід математики оголошують помилковим. Багато фахівців з теорії ймовірностей мало не зробили своєю професією пошуки чужих помилок. На жаль, проти їх суджень не заперечиш. Принаймні, в негативній їх частині. І в цьому друге «але». Майже неможливо вибрати математичний метод, захищений від критики. Значить, ніякої «суворої наукової основи» математика запропонувати не може. Її строгість удавана.

МАТЕМАТИК: – всі твої випади мітять не в математику, а в приклади її некомпетентного використання. З цих позицій можна засудити будь-яку науку, від біохімії до естетики. Колись хтось сказав, що існують три види брехні: просто брехня, нахабна брехня і статистика. Зрозуміло, він мав на увазі спекуляцію фактами, засновану на статистичній фразеології. А що стосується сигарет, то можеш не самовтішатися: тут висновки зроблені з наукової точки зору бездоганно. І смішно проводити паралель між цими висновками і вишукуваннями вічного двигуна або рецептів виграшу в «Спортлото».

СКЕПТИК: – до речі про «Спортлото». Ти впевнений, що в цій грі немає розумної стратегії?

МАТЕМАТИК: – твоє питання саме по собі більше викриває в тобі невігласа, ніж твої колкості: згідно з математикою, однаково можлива будь-яка комбінація чисел. Ти не зможеш збільшити ймовірність виграшу, прийнявши якусь стратегію.

СКЕПТИК: — ось типова роль математика – ковзає над гладдю явищ, не зачіпаючи їх серцевини. Ти забув, що крім ймовірності виграшу важливий ще і його розмір. А розмір можна підвищити, призначаючи ті комбінації чисел, проти яких багато упереджені. Наприклад, мало хто призначає перші шість номерів по порядку – так призначай їх постійно, з тиражу в тираж. І тобі буде ні з ким ділити виграш.

МАТЕМАТИК: – Ось це гідна тебе область наукової творчості. Браво! Чи не запропонуєш чогось з приводу вічного двигуна?

СКЕПТИК (вдаючи, що не чув): — однак забалакався я з тобою, а справа не чекає. Так, стривай. (Вже майже пішовши, повертається). Навіщо – то ти був мені потрібен. А ось навіщо? Ах, чорт! Згадав! Скажи, будь ласка, як мені переконатися в репрезентативності вибірки ось в цьому експерименті? (Розгортає згорнутий трубочкою папір.)

МАТЕМАТИК: – тобі хочеться дізнатися істину або просто заткнути глотки можливим опонентам?

СКЕПТИК (бентежачись): – бачиш, у висновку я, взагалі кажучи, впевнений. Але мені потрібно статистичне обгрунтування того, що я провів достатню кількість дослідів, ну, там з урахуванням розкиду даних та іншого. Так допоможеш?

МАТЕМАТИК: – Ага, тебе цікавить в математиці її «забійна сила». Так от: я не стану постачати тебе нею. По-перше, ти тільки що сам іронізував над таким застосуванням математичних знань. По-друге, математика не знає безперечної відповіді на твоє запитання. І по-третє, у мене теж немає часу.

СКЕПТИК (йдучи бурмоче):- досить було «по-друге».

Автор: М. Висотський.