Закони азарту і математика
Стаття написана Павлом Чайкою, головним редактором журналу «Пізнавайка». З 2013 року з моменту заснування журналу Павло Чайка присвятив себе популяризації науки в Україні та світі. Основна мета як журналу, так і цієї статті – пояснити складні наукові теми простою та доступною мовою.
У 1654 році до знаменитого математика і фізика Блеза Паскаля звернувся за консультацією лейтенант роти мушкетерів. Відвідувач був пристрасним гравцем у кістки. Під принципи своєї гри він намагався підвести наукову базу. Мушкетер виявив, що якщо кидати кістку чотири рази, чекаючи, що хоч якось випаде шістка, завжди залишаєшся у виграші, якщо граєш досить довго. Але якщо кидати відразу дві кістки двадцять чотири рази, сподіваючись на випадання двох шісток одночасно, то зазвичай програєш, як би довго не грав.
Ця обставина викликала у гравця подив. Він вважав, що розуміється в математиці, і ніяк не міг второпати, чому при грі в кістки невірна пропорція 4:6 = 24:36. Паскаль зацікавився цією проблемою. До речі, займаючись нею, він заклав основи теорії ймовірності.
З розрахунків великого вченого випливало, що якщо кидати m кісток відразу, ймовірність випадання m шісток при числі кидання n виражається формулою:
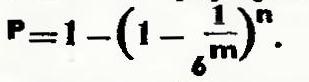
Підставляючи замість m 1, а замість n 4, отримаємо, що вірогідність виграшу Р дорівнює 0,518. Оскільки це більше, ніж 1/2, грати так вигідно для кидаючого. А тепер підставимо замість m 2, а замість n 24. У цьому випадку ймовірність виграшу становить лише 0,491. Іншими словами, при такій системі гри програш закономірний.
Висновки теорії ймовірності абсолютно вірні лише при нескінченно великому числі кидання. Це відноситься до гри не тільки в кістки, але і в орлянку, в рулетку, тощо. При кінцевому числі кидання можуть бути самі неймовірні відхилення від прогнозів теорії.
В історії знаменитого казино в Монте-Карло відомий випадок, коли з двох можливих кольорів один випадав поспіль 28 разів. У гральному закладі Саратога в Нью-Йорку кулька рулетки зупинялася на червоному полі 32 рази поспіль. Теорія передбачає: щоб гарантовано отримати такий результат, кожен з тисячі гравців повинен ставити на червоне по 250 раз в день протягом 50 років!
Закони випадку вельми примхливі. Часом завдяки цьому відбуваються кумедні історії. Ось одна з них.
Якось американський інженер Річард Ярецький, фахівець в області обчислювальної техніки, прийшов до думки, що висновки теорії ймовірності не зовсім застосовні до гри в рулетку. Зупинка кульки на тому чи іншому полі залежить не тільки від випадковості. Механізм рулетки не ідеальний. Кулька, що кидається рукою круп’є, залишає непомітні вм’ятини на бортах. Ці вм’ятини впливають на рух інших кульок. У розташуванні їх повинна бути закономірність – адже у кожного круп’є свій, характерний лише для нього спосіб кидання. Тому на столі, за яким багато грали і який обслуговується одним якимось круп’є, деякі номери мають випадати частіше, ніж це було б з теорії ймовірності.
Ярецький пропонував багатьом американським мільйонерам купити у нього таємницю вірного виграшу в рулетку, але йому ніхто не вірив. Тоді він вирішив сам стати гравцем. Зрозуміло, щасливим гравцем.
Разом з двома своїми друзями він протягом півтора місяців щодня відвідував казино в Баден-Бадені (Німеччина). Всі номера, що випадали при киданні записувалися. Список вийшов значним – він охоплював 20 тисяч кидків. Ярецький послав його в Лондонський обчислювальний центр. Електронний мозок проаналізував список і зазначив номера, у яких кулька зупинялася особливо часто.
Ну, а потім троє математиків взялися за гру. За кілька днів вони привели казино до банкрутства, вигравши 750 тисяч доларів!
Автор: Павло Чайка, головний редактор журналу Пізнавайка
При написанні статті намагався зробити її максимально цікавою, корисною та якісною. Буду вдячний за будь-який зворотний зв'язок та конструктивну критику у вигляді коментарів до статті. Також Ваше побажання/питання/пропозицію можете написати на мою пошту pavelchaika1983@gmail.com або у Фейсбук.